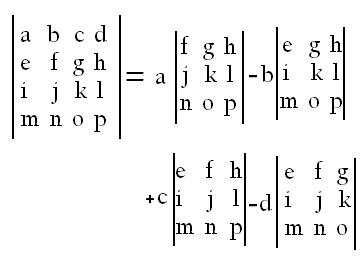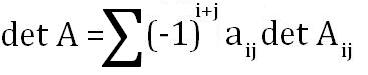پیش از هر چیز یادآوری میکنم تعریف پایه در فضاهای برداری و مدولها مشابه هستند: «پایه یک مجموعه مولد فضا است که مستقل خطی نیز باشد».
در این مجال قصد بررسی تعمیم دو خاصیت از فضاهای برداری به مدولها را داریم، این خصوصیات عبارتند از:
-
هر مجموعه مولد فضا شامل یک پایه است
-
در یک فضای بردای هر مجموعه مستقل خطی را میتوان به یک پایه تعمیم داد
-
کاردینال پایه یک فضای برداری خوشتعریف است
حال در مدولها بررسی را انجام میدهیم:
-
را به عنوان یک
مولد هست ولی چون مستقل خطی نیست (چرا؟) لذا نمیتواند به یک پایه تعمیم پیدا کند.
-
فرض کنیدV یک فضای برداری نامتناهی البعد باشد و
(حلقه همه تبدیلات خطی از V به V)، حال R را به عنوان R-مدول مورد بررسی قرار میدهیم.
تعریف میکنیم:
برای هر i بزرگتر از 1:
مجموعه
یک مجموعه مستقل خطی را تشکیل میدهد ولی این فضا هیچ پایه نامتناهی ندارد (زیرا دارای حداقل یک پایه متناهی
است.) میتوانید به آسانی بررسی کنید که
-
R را همان R فوق در نظر بگیرید؛ مجموعه
(که
همان قبلی است) پایه‌ای برای R تشکیل میدهد ولذا بعد در مدول خوشتعریف نیست!
با توجه به اینکه بیشتر مخاطبین این مطلب دوستانی هستند که از طریق موتورهای جست و جو وارد وبلاگ شدهاند، صفحاتی را برای این دوستان پیشنهاد میکنم تا مطالعه کنند:
مطالب پیشنهادی:
